Calculus &
Linear Algebra II

Chapter 1

1 Solutions of first order ODEs

By the end of this section, you should be able to answer the following questions about first order ODEs:

  • How do you solve an IVP associated with directly integrable, separable or linear ODEs? (Revision)
  • Under what conditions does a solution to an IVP problem exist?
  • Under what conditions is a solution to an IVP problem unique?

In MATH1052, you were introduced to Ordinary Differential Equations (ODEs) and Initial Value Problems (IVPs) and saw how to find solutions to some special types of first order equations. In particular, there should be three types of first order ODEs that you are familiar with solving.



1 Solutions of first order ODEs

In MATH1052, you were introduced to Ordinary Differential Equations (ODEs) and Initial Value Problems (IVPs) and saw how to find solutions to some special types of first order equations. In particular, there should be three types of first order ODEs that you are familiar with solving.

• Directly integrable: $\dfrac{dy}{dx} = f(x)$

• Separable: $\dfrac{dy}{dx} = f(x)g(y)$

• Linear: $\dfrac{dy}{dx} = q(x)-p(x)~y$




1 Solutions of first order ODEs

• Directly integrable: $\dfrac{dy}{dx} = f(x)$

$\displaystyle \dfrac{dy}{dx}~dx = f(x) ~dx $ $\displaystyle \;\;\Rightarrow \;\; dy = f(x) ~dx $

$\displaystyle \;\;\Rightarrow \;\; y =\int f(x)~dx + C $






1 Solutions of first order ODEs

• Separable: $\dfrac{dy}{dx} = f(x)g(y)$

$\displaystyle \dfrac{1}{g\left(y\right)}\dfrac{dy}{dx} = f(x) $ $\displaystyle \;\;\Rightarrow \;\; \dfrac{1}{g\left(y\right)}\dfrac{dy}{dx} dx = f(x) ~dx $

$\displaystyle \;\;\Rightarrow \;\; \dfrac{1}{g\left(y\right)}~dy = f(x) ~dx $ $\displaystyle \;\;\Rightarrow \;\; \int \dfrac{1}{g\left(y\right)}~dy = \int f(x) ~dx +C $


Note: Here we have an implicit solution.



1 Solutions of first order ODEs

• Linear: $\dfrac{dy}{dx} = q(x)-p(x)~y$

First, we need to write it in standard form: \[ \frac{dy}{dx} + p(x) y = q(x). \]

Multiply by $I(x) \neq 0$ to obtain

$ \ds I(x) \frac{dy}{dx} + I(x) p(x) y = I(x)q(x). $


1 Solutions of first order ODEs

• Linear: $\dfrac{dy}{dx} = q(x)-p(x)~y$

$\ds I(x) \frac{dy}{dx} + I(x) ~p(x)~ y = I(x)~q(x).$

We choose $I(x)$ such that $\frac{d}{dx}\big(I(x)~y\big) = I(x)~ q(x).$

Integrating we obtain   $ \ds I(x)~y = \int I(x)~q(x)~dx + C. $

That is   $ \ds y = \frac{1}{I(x)}\int I(x)~q(x)~dx + \frac{C}{I(x)}. $


Note: $I(x) = \exp\left(\int p(x)~dx\right)$ is the integrating factor.


1 Solutions of first order ODEs

In most applications involving first order ODEs, we are required to solve an IVP. Generally, this is a problem of the form \[ \frac{dy}{dx}=f(x,y), \quad y(x_0 )= y_0. \]

In other words, we seek to find solutions of the ODE which pass through the point $(x_0, y_0)$ in the $x$-$y$ plane.




1.1 Example: $\ds \frac{dy}{dx}= x, y(0) = 1$ has a unique solution

Integrating: $\ds y = \int x ~dx + C$ $\,=\ds \frac{1}{2}x^2 + C$

Let's solve now the Initial Value Problem (IVP): $y(0)=1 $ $\Rightarrow 1 = \frac{1}{2}(0)^2 + C$ $ \Rightarrow C = 1$.

Therefore \[ y = \frac{1}{2}x^2 + 1. \]



1.1 Example: $\ds \frac{dy}{dx}= x, y(0) = 1$ has a unique solution

$\ds y = \frac{1}{2}x^2 + 1.$

GeoGebra commands for
Slope field and ODE Solution: 


										SlopeField(x)

										SolveODE(x, 0, 1, 8, 0.001)




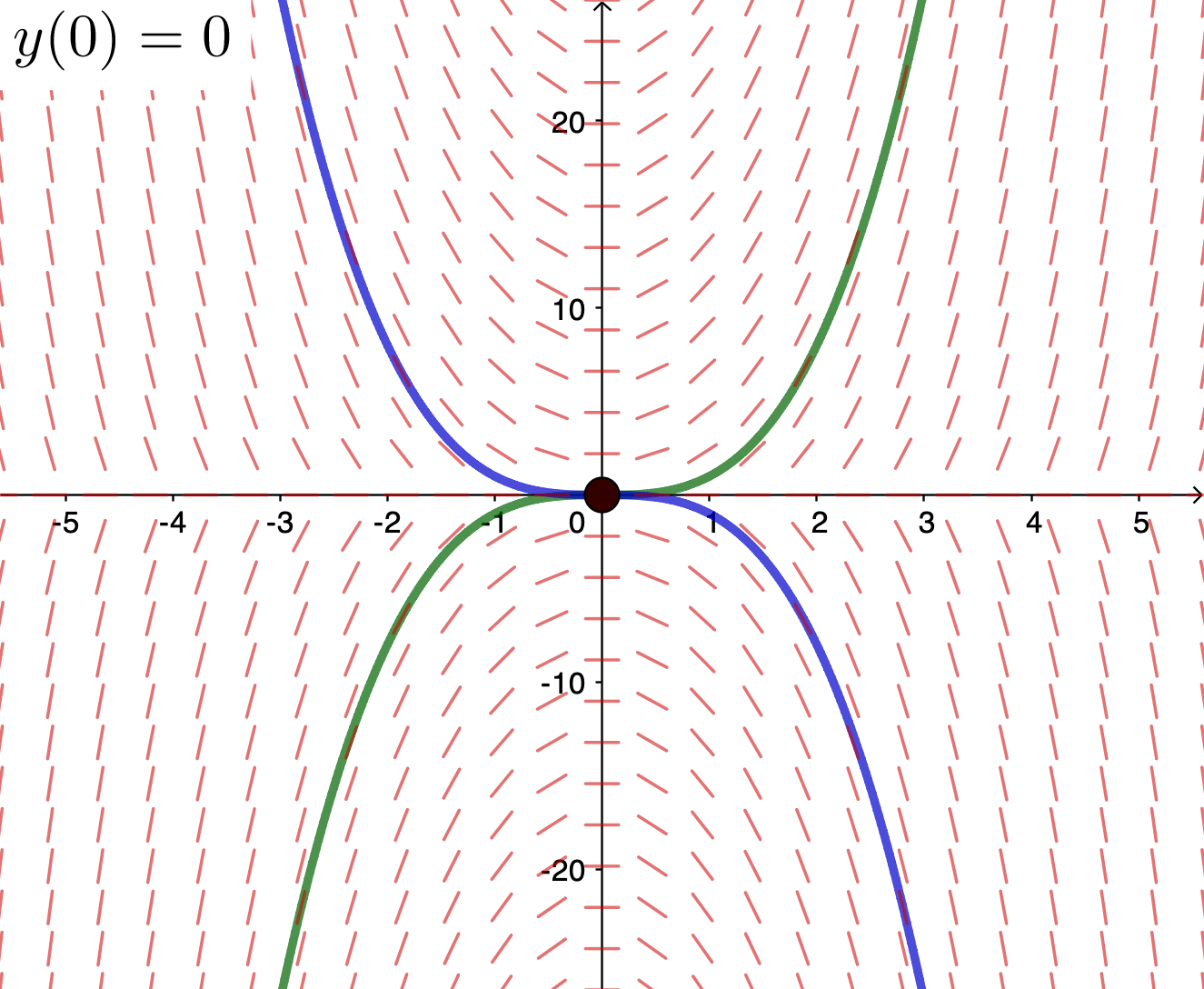
1.2 Example: $\ds \frac{dy}{dx}= 3xy^{1/3}, y(0) = 0$ has more than one solution

This is a separable ODE: So $\, \ds \frac{dy}{y^{1/3}}=3x $
Integrating we have $\, \ds \Rightarrow \frac{3}{2}y^{2/3}=\frac{3}{2}x^2 + C$

Let's solve now the IVP: $y(0)=0 $ $\;\Rightarrow \;\ds \frac{3}{2}(0)^{2/3}=\frac{3}{2}(0)^2 + C$ $ \;\Rightarrow\; C = 0$ $ \;\Rightarrow\; y^2 = \left(x^2\right)^3$ $ \, = x^6$.

Therefore \[ y = x^3 \quad \text{ or } \quad y = - x^3. \]


1.2 Example: $\ds \frac{dy}{dx}= 3xy^{1/3}, y(0) = 0$ has more than one solution

$\ds y = x^3 \quad \text{ or } \quad y = - x^3.$

GeoGebra commands for
Slope field and ODE Solution: 


										f(x,y) = 3*x*y^(1/3)

										SlopeField(f)

										SolveODE(f, 0, 0, 8, 0.001)

What is going on? 🤔




1.2 Example: $\ds \frac{dy}{dx}= 3xy^{1/3}, y(0) = 0$ has more than one solution

$\ds y = x^3 \quad \text{ or } \quad y = - x^3.$

What is going on? 🤔

Here the computer cannot help us! 😢





1.3 Example: $\ds \frac{dy}{dx}= \frac{x-y}{x}, y(0) = 1$ has no solution

Note that the ODE is linear: $\, \ds \frac{dy}{dx} + \dfrac{y}{x}=1$

Multiply by $x$: $\, \Ra \;\ds x\frac{dy}{dx} + y=x$ $\, \Ra \;\ds \dfrac{d}{dx}\big(xy\big)=x$

Here the factor $x$ is the Integrating factor,

that is, $\;I(x) =\ds \exp\left({\int \,\frac{1}{x}\,dx}\right) $ $= x$




1.3 Example: $\ds \frac{dy}{dx}= \frac{x-y}{x}, y(0) = 1$ has no solution

Note that the ODE is linear: $\, \ds \frac{dy}{dx} + \dfrac{y}{x}=1$

Multiply by $x$: $\, \Ra \;\ds x\frac{dy}{dx} + y=x$ $\, \Ra \;\ds \dfrac{d}{dx}\big(xy\big)=x$

$\, \Ra \; xy = \ds \frac{1}{2}x^2 +C$   or $\; \ds y = \frac{1}{2}x+ \frac{C}{x}.$





1.3 Example: $\ds \frac{dy}{dx}= \frac{x-y}{x}, y(0) = 1$ has no solution

Thus the general solution of the linear ODE $\, \ds \frac{dy}{dx} + \dfrac{y}{x}=1$ is $$ \ds y = \frac{1}{2}x+ \frac{C}{x}.$$

Can we solve the IVP: $y(0)=1$? Note that $\ds \frac{C}{x}\to \infty $ when $x \ra 0$.

How about choosing $C=0$? But then $y(0)=0$. 😕

Then it cannot satisfy the initial condition. Therefore, no solution satisfies $y(0)=1$.



1.3 Example: $\ds \frac{dy}{dx}= \frac{x-y}{x}, y(0) = 1$ has no solution

No solution satisfies $y(0)=1$.

GeoGebra commands for
Slope field and ODE Solution: 


										f(x,y) = (x-y)/x

										SlopeField(f)

										SolveODE(f, 0, 0, 8, 0.001)

Same issue with technology! 🤔




1.4 Existence and uniqueness criteria

Here we consider the initial value problem of the form \[ \frac{dy}{dx}=f(x,y), \quad y(x_0)=y_0. \]

The main result concerns the conditions under which we have existence and uniqueness of a solution.

  • (existence) If $f(x, y)$ is continuous in some rectangle \[ R =\left\{(x,y) ~|~ |x-x_0|\lt a, |y-y_0|\lt b|\right\} \] then the initial value problem has at least one solution.
  • (uniqueness) Moreover, if $f_y(x, y)$ is also continuous in $R$ then there is some interval $|x-x_0|\leq h \lt a$ which contains a unique solution to the initial value problem.


1.4 Existence and uniqueness criteria

  • (existence) If $f(x, y)$ is continuous in some rectangle \[ R =\left\{(x,y) ~|~ |x-x_0|\lt a, |y-y_0|\lt b|\right\} \] then the initial value problem has at least one solution.
  • (uniqueness) Moreover, if $f_y(x, y)$ is also continuous in $R$ then there is some interval $|x-x_0|\leq h \lt a$ which contains a unique solution to the initial value problem.

This result only tells us that a solution exists or is unique locally (i.e., in the rectangle $R$). Beyond $R$, we simply don't know. Let's look at the previous three examples in the context of the two conditions. In the next section, we look closer at understanding these conditions and how they arise.



1.5 Example: $\ds \frac{dy}{dx}= x, y(0) = 1$

Here $f(x,y) = x$   is continuous and  $\ds \frac{\partial f}{\partial y} = 0$   is continuous.

This implies a unique solution: $y =\ds\frac{1}{2}x^2 + 1.$







1.6 Example: $\ds \frac{dy}{dx}= 3xy^{1/3}, y(0) = 0$

For $(x_0,y_0)=(0,0)$,   $f(x,y) = 3xy^{1/3}$   is continuous, then the solution exists.

On the other hand we have $\ds \frac{\partial f}{\partial y} = \frac{x}{y^{2/3}}.$ This is not continuous in any rectangle containing $(0,0).$

Therefore, we cannot comment on uniqueness. In fact we have that $y=\pm x^3.$




1.6 Example: $\ds \frac{dy}{dx}= 3xy^{1/3}, y(0) = 0$

1.7 Example: $\ds \frac{dy}{dx}= \frac{x-y}{x}, y(0) = 1$

Here $\;f(x,y) = \dfrac{x-y}{x}$   is not continuous in any rectangle containing $(0,1).$

Therefore, we cannot comment on existence.






1.7 Example: $\ds \frac{dy}{dx}= \frac{x-y}{x}, y(0) = 1$


Credits