Mathematical Analysis
Lecture 4
2.3.2 Algebraic properties
Theorem 2.3.3. Let $\{ x_n \}$ and $\{ y_n \}$ be convergent sequences.
1. The sequence $\{ z_n \}$, where $z_n := x_n \pm y_n$, converges and
$\ds \lim_{n \to \infty} (x_n \pm y_n) $ $\ds = \lim_{n \to \infty} z_n $ $\ds = \lim_{n \to \infty} x_n \pm \lim_{n \to \infty} y_n .$
2. The sequence $\{ z_n \}$, where $z_n := x_n y_n$, converges and
$\ds \lim_{n \to \infty} (x_n y_n) $ $\ds =\lim_{n \to \infty} z_n $ $\ds =\left( \lim_{n \to \infty} x_n \right) \left( \lim_{n \to \infty} y_n \right) .$
2.3.2 Algebraic properties
Theorem 2.3.3. Let $\{ x_n \}$ and $\{ y_n \}$ be convergent sequences.
- If $\lim\, y_n \not= 0$ and $y_n \not= 0$ for all $n \in \N$, then the sequence $\{ z_n \}$, where $z_n := \dfrac{x_n}{y_n}$, converges and \begin{equation*} \lim_{n \to \infty} \frac{x_n}{y_n} = \lim_{n \to \infty} z_n = %\frac{\lim_{n \to \infty} x_n}{\lim_{n \to \infty} y_n} . \frac{\lim\, x_n}{\lim\, y_n} . \end{equation*}
- If $x_n \geq 0$, then \begin{equation*} \lim_{n\to\infty} \sqrt{x_n} = \sqrt{ \lim_{n\to\infty} x_n } . \end{equation*}
Proof of Theorem 2.3.3, Item 2.
Proof. Suppose that $\{ x_n \}$ and $\{ y_n \}$ are convergent sequences and write $z_n := x_n y_n$. Let $x := \lim\, x_n$, $y := \lim\, y_n$.
To prove that $x_n y_n$ converges to $xy$ we make the estimate
$\abs{x_ny_n - xy}$ $= \abs{\left( x_n y_n -x_n y\right) +\left( x_n y -xy\right) }$
$\qquad\quad \;\;\;\;\leq \abs{x_n\left(\, y_n - y\right) } + \abs{y\left( x_n -x\right) }$
$\qquad\quad\;\;\;\; = \abs{x_n}\abs{\, y_n - y } + \abs{y}\abs{x_n -x }.$
Proof of Theorem 2.3.3, Item 2.
Proof. 👉 $\,\abs{x_ny_n - xy} \leq \abs{x_n}\abs{\, y_n - y } + \abs{y}\abs{x_n -x }.$
Since $\{x_n\}$ is convergent, there exists a real number $M_1\gt 0$ such that $\abs{x_n}\leq M_1$ for all $n\in \N$ (according to Theorem 2.1.2). We set $$M:= \max \left\{M_1, |y|\right\}.$$ Then we have
$\abs{x_ny_n - xy } \leq M \abs{y_n-y} + M \abs{x_n-x}$
Proof of Theorem 2.3.3, Item 2.
Proof.
$\abs{x_ny_n - xy } \leq M \abs{y_n-y} + M \abs{x_n-x}$
Since $x_n$ and $y_n$ converge, we conclude that if $\vre \gt 0$ is given, then there exist natural numbers $K_1$ and $K_2$ such that
if $n\geq K_1$ then $\abs{x_n-x}\lt \dfrac{\vre}{2M}$, and
if $n\geq K_2$ then $\abs{y_n-y}\lt \dfrac{\vre}{2M}.$
Proof of Theorem 2.3.3, Item 2.
Proof.
if $n\geq K_1$ then $\abs{x_n-x}\lt \dfrac{\vre}{2M}$, and
if $n\geq K_2$ then $\abs{y_n-y}\lt \dfrac{\vre}{2M}.$
$\abs{x_ny_n - xy } \leq M \abs{y_n-y} + M \abs{x_n-x} \qquad \quad$
$\quad \quad \;\;\;\;\ds\leq M \left(\frac{\vre}{2M}\right) + M \left(\frac{\vre}{2M}\right)$ $=\vre$
Since $\vre \gt 0$ is arbitrary, this proves that the sequence $z_n = x_ny_n$ converges to $xy.$ $\; \blacksquare$
Some corollaries
By plugging in constant sequences in the previous Theorem, we get several easy corollaries. If $c \in \R$ and $\{ x_n \}$ is a convergent sequence, then for example
$\ds \lim_{n \to \infty} c x_n = c \left( \lim_{n \to \infty} x_n \right), \;$ and
$\ds \lim_{n \to \infty} (c + x_n) = c + \lim_{n \to \infty} x_n .$
Similarly, we find such equalities for constant subtraction and division.
Some corollaries
As we can take limits past multiplication we can show that $$\lim\, x_n^k = {(\lim\, x_n)}^k \;\text{for all }\; k \in \N.$$ Finally, we can also show a similar result for the $k$th roots (which is more challenging to prove). That is, $$\ds\lim\, x_n^{1/k} = {(\lim\, x_n)^{1/k}} \; \text{for all }\;k \in \N.$$
Example 2.3.2
Define $\{x_n\}$ recursively by $ \ds x_1 := 2, \, x_{n+1} := x_n - \frac{x_n^2-2}{2x_n} . $
Does $\{x_n\}$ converge? 🤔
Example 2.3.2
Define $\{x_n\}$ recursively by $ \ds x_1 := 2, \, x_{n+1} := x_n - \frac{x_n^2-2}{2x_n} . $
Claim 1: $\{x_n\}$ is bounded below. Use induction.
1. $x_1 = 2>0.$
2. Assume $x_n\gt 0.$
3. $x_{n+1}$ $= x_n-\dfrac{x_n^2-2}{2x_n}$ $= \dfrac{2x_n^2-x_n^2+2}{2x_n}$ $= \dfrac{x_n^2+ 2}{2x_n}$ $\gt 0.$
Example 2.3.2
Define $\{x_n\}$ recursively by $ \ds x_1 := 2, \, x_{n+1} := x_n - \frac{x_n^2-2}{2x_n} . $
Claim 2: $\{ x_n \}$ is monotone decreasing. If we show that $x_n^2- 2 \geq 0$ for all $n$, then $x_{n+1}\leq x_n$ for all $n$.
Note that $x_1^2-2= 4-2$ $= 2>0.$
Now for an arbitrary $n$ we have
$\ds x_{n+1}^2-2 = {\left( \frac{x_n^2+2}{2x_n} \right)}^2 - 2$ $\ds = \frac{x_n^4+4x_n^2+4 - 8x_n^2}{4x_n^2}$ $\ds= \frac{x_n^4-4x_n^2+4}{4x_n^2}$ $\ds = \frac{{\left( x_n^2-2 \right)}^2}{4x_n^2} .$
Example 2.3.2
Define $\{x_n\}$ recursively by $ \ds x_1 := 2, \, x_{n+1} := x_n - \frac{x_n^2-2}{2x_n} . $
Claim 2: $\{ x_n \}$ is monotone decreasing. If we show that $x_n^2- 2 \geq 0$ for all $n$, then $x_{n+1}\leq x_n$ for all $n$.
👉 $\;\ds x_{n+1}^2-2 $ $\ds = \frac{{\left( x_n^2-2 \right)}^2}{4x_n^2} .$
Since squares are nonnegative, $x_{n+1}^2-2 \geq 0$ for all $n$.
Therefore, $\{ x_n \}$ is monotone decreasing and bounded, and so the limit exists.
Example 2.3.2
Define $\{x_n\}$ recursively by $ \ds x_1 := 2, \, x_{n+1} := x_n - \frac{x_n^2-2}{2x_n} . $
Claim 3: $\lim x_n = \sqrt{2}$.
Set $L := \lim x_n.$ Then
$\ds x_{n+1} = x_n - \frac{x_n^2-2}{2x_n}$ $\Rightarrow \ds \lim x_{n+1} =\lim x_n - \frac{ \lim x_n^2-2}{ 2 \lim x_n}$ $\Rightarrow \ds L =L - \frac{ L^2-2}{ 2 L}$ $\Rightarrow \ds 0 = \frac{ L^2-2}{ 2 L}$ $\Rightarrow \ds L^2-2=0$
$L = \pm\sqrt{2}.\,$ But $x_n\gt 0$ for all $n.$ So $\,L = \lim x_n = \sqrt{2}.$
2.3.3 Some convergence tests
Theorem 2.3.4. Let $\{ x_n \}$ be a sequence. Suppose there is an $x \in \R$ and a convergent sequence $\{ a_n \}$ such that \begin{equation*} \lim_{n\to\infty} a_n = 0 \quad \text{ and } \quad \abs{x_n - x} \leq a_n \quad \text{for all $n \in \N$.} \end{equation*} Then $\{ x_n \}$ converges and $\lim\, x_n = x$.
Theorem 2.3.5. Let $c > 0$.
- If $c \lt 1$, then $\lim_{n\to\infty} c^n = 0.$
- If $c \gt 1$, then $\{ c^n \}$ is unbounded.
2.3.3 Some convergence tests
Theorem 2.3.6. (Ratio test for sequences) Let $\{ x_n \}$ be a sequence such that $x_n \not= 0$ for all $n$ and such that the limit \begin{equation*} L := \lim_{n\to\infty} \frac{\abs{x_{n+1}}}{\abs{x_n}} \qquad \text{exists.} \end{equation*}
- If $L \lt 1$, then $\{ x_n \}$ converges and $\lim\, x_n = 0$.
- If $L \gt 1$, then $\{ x_n \}$ is unbounded (hence diverges).
2.4.1 Upper & lower limits
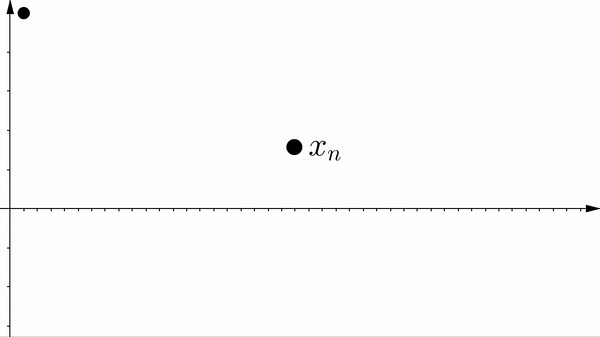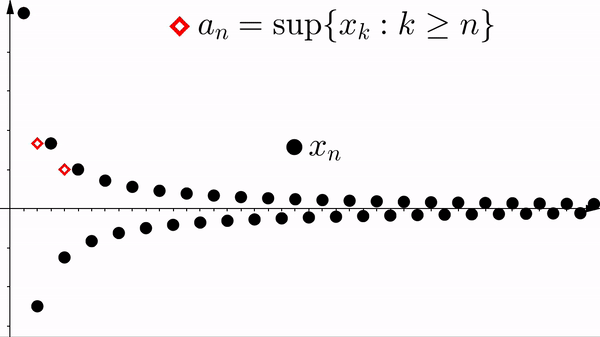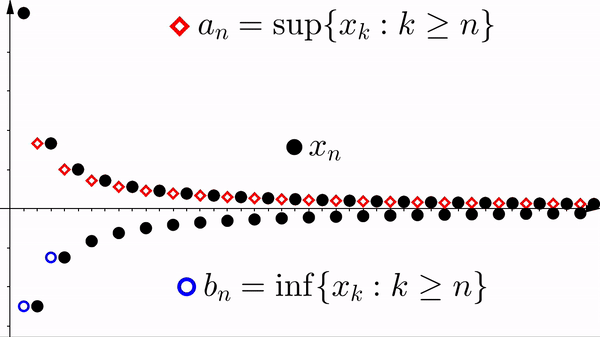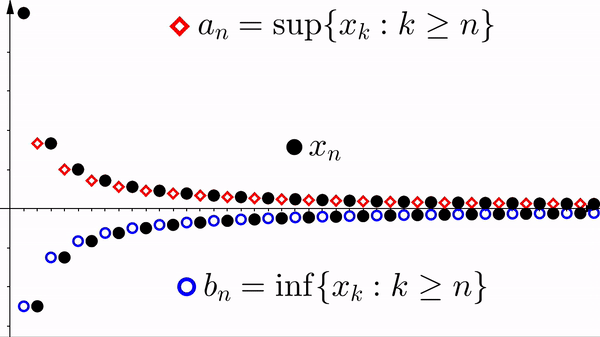
Definition 2.4.1. Let $\{ x_n \}$ be a bounded sequence. Define the sequences $\{ a_n \}$ and $\{ b_n \}$ by
$a_n := \sup \{ x_k : k \geq n \}$ and $b_n := \inf \{ x_k : k \geq n \}$.
Define, if the limits exist,
Limit superior: $\,\ds \limsup_{n \to \infty} \, x_n := \lim_{n \to \infty} a_n , $
Limit inferior: $\,\ds \liminf_{n \to \infty} \, x_n := \lim_{n \to \infty} b_n . $
2.4.1 Upper & lower limits
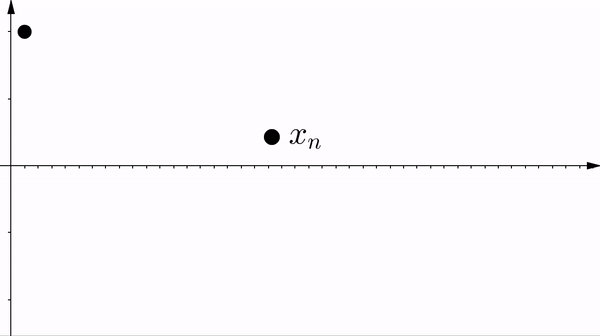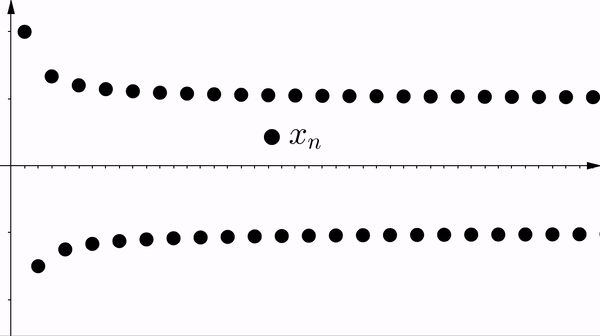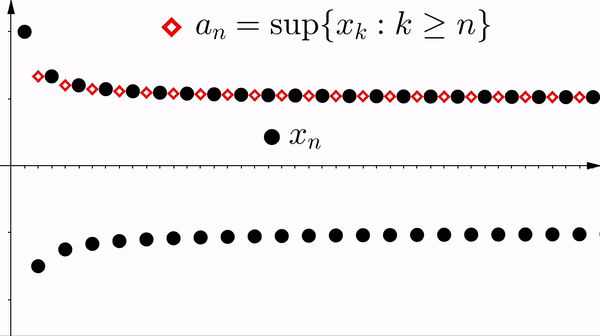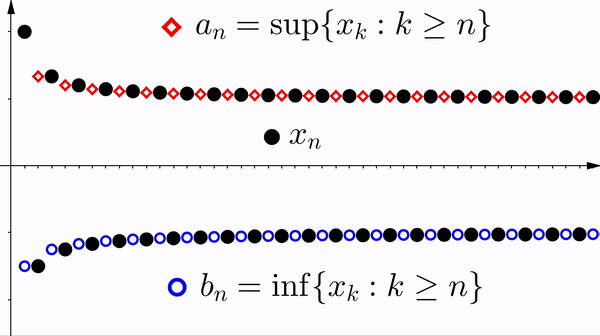
$x_n$ is bounded.
2.4.1 Upper & lower limits
Theorem 2.4.1. Let $\{ x_n \}$ be a bounded sequence. Let $a_n$ and $b_n$ be as in the definition above.
- The sequence $\{ a_n \}$ is bounded monotone decreasing and $\{ b_n \}$ is bounded monotone increasing. In particular, $\liminf x_n$ and $\limsup x_n$ exist.
- $\displaystyle \limsup_{n \to \infty} \, x_n = \inf \{ a_n : n \in \N \}$ and $\displaystyle \liminf_{n \to \infty} \, x_n = \sup \{ b_n : n \in \N \}$.
- $\displaystyle \liminf_{n \to \infty} \, x_n \leq \limsup_{n \to \infty} \, x_n$.
2.4.1 Upper & lower limits
Proof. The sequence $\{ a_n \}$ is bounded monotone decreasing and $\limsup x_n = \inf \{ a_n : n \in \N \}$ exist.
Note that $\{a_n\}$ is bounded below (since $\{x_n\}$ is) and monotone decreasing:
$a_{n+1} = \sup \{x_n : k\geq n+1 \}$ $\leq \sup \{x_n : k\geq n \}$ $= a_n.$
Taking $\sup$ of a subset is always $\leq$ than $\sup$ of the whole set. Hence $\{a_n\}$ converges.
The rest of the proof is left as an exercise 📝 or check the 👀 Complementary reading 📖
Example 2.4.1
Let $\{ x_n \}$ be defined by \begin{equation*} x_n := \begin{cases} \dfrac{n+1}{n} & \text{if } n \text{ is odd,} \\ 0 & \text{if } n \text{ is even.} \end{cases} \end{equation*}
First the limit inferior:
$\ds \liminf_{n\to\infty} \, x_n$ $= \ds \lim_{n\to\infty} \bigl( \inf \{ x_k : k \geq n \} \bigr)$ $=\ds \lim_{n\to\infty} 0 $ $=0$
Example 2.4.1
Let $\{ x_n \}$ be defined by \begin{equation*} x_n := \begin{cases} \dfrac{n+1}{n} & \text{if } n \text{ is odd,} \\ 0 & \text{if } n \text{ is even.} \end{cases} \end{equation*}
For the limit superior, we write
$\ds\limsup_{n\to\infty} \, x_n = \lim_{n\to\infty} \bigl( \sup \{ x_k : k \geq n \} \bigr) .$
In fact $\; \ds \sup \{ x_k : k \geq n \} = \begin{cases} \ds\frac{n+1}{n} & \text{if } n \text{ is odd,} \\ \ds\frac{n+2}{n+1} & \text{if } n \text{ is even.} \end{cases} \;$ 📝
Example 2.4.1
Let $\{ x_n \}$ be defined by \begin{equation*} x_n := \begin{cases} \dfrac{n+1}{n} & \text{if } n \text{ is odd,} \\ 0 & \text{if } n \text{ is even.} \end{cases} \end{equation*}
Thus we have that
$\ds\limsup_{n\to\infty} \, x_n = \lim_{n\to\infty} \bigl( \sup \{ x_k : k \geq n \} \bigr)$ $=1$
Note that $\{x_n\}$ does not converge.
2.4.1 Upper & lower limits
Theorem 2.4.3. Let $\{ x_n \}$ be a bounded sequence. Then $\{ x_n \}$ converges if and only if \begin{equation*} \liminf_{n\to \infty} \, x_n = \limsup_{n\to \infty} \, x_n. \end{equation*} Furthermore, if $\{ x_n \}$ converges, then \begin{equation*} \lim_{n\to \infty} x_n = \liminf_{n\to \infty} \, x_n = \limsup_{n\to \infty} \, x_n. \end{equation*}
👀 Complementary reading 📖
2.4.1 Upper & lower limits
$x_n$ is bounded and convergent.
2.5 Bolzano-Weierstrass' theorem
Theorem 2.5.1 (Bolzano-Weierstrass) Suppose a sequence $\{ x_n \}$ of real numbers is bounded. Then there exists a convergent subsequence $\{ x_{n_i} \}$.
👀 Complementary reading 📖
2.6 Cauchy sequences
Definition 2.6.1. A sequence $\{ x_n \}$ is a Cauchy sequence if for every $\vre > 0$ there exists an $N \in \N$ such that for all $n \geq N$ and all $k \geq N$, we have \begin{equation*} \abs{x_n - x_k} \lt \vre . \end{equation*}
2.6 Cauchy sequences

If for every $\epsilon > 0$ there exists an $M \in \N$ such that
for all $n \geq M$ and all $k \geq M$, we have $\abs{x_n - x_k} \lt \epsilon .$
2.6 Cauchy sequences
Theorem 2.6.1. A Cauchy sequence is bounded.
Theorem 2.6.2. A sequence of real numbers is Cauchy if and only if it converges.

👀 Complementary reading 📖
Example 2.6.1
Claim: The sequence $\left\{ \dfrac{1}{n} \right\}$ is a Cauchy sequence.
Proof. Given $\vre \gt 0$, find $N$ such that $N \gt \dfrac{2}{\vre}$. Then for $n,k \geq N$, we have $\dfrac{1}{n} \lt \dfrac{\vre}{2}$ and $\dfrac{1}{k} \lt \dfrac{\vre}{2}$. Therefore, for $n, k \geq N$, we have
$\ds \abs{\frac{1}{n} - \frac{1}{k}}$ $\ds\leq \abs{\frac{1}{n}} + \abs{\frac{1}{k}}$ $\ds\lt \frac{\vre}{2} + \frac{\vre}{2}$ $= \vre. \; \blacksquare$
Example 2.6.2
Claim: The sequence $\left\{ \dfrac{n+1}{n} \right\}$ is a Cauchy sequence.
Proof. Given $\vre \gt 0$, find $N$ such that $N \gt \dfrac{2}{\vre}$. Then for $n,k \geq N$, we have $\dfrac{1}{n} \lt \dfrac{\vre}{2}$ and $\dfrac{1}{k} \lt \dfrac{\vre}{2}.$ Therefore, for $n, k \geq N$, we have
$\ds \abs{\frac{n+1}{n} - \frac{k+1}{k}}$
$\ds=
\abs{\frac{k-n}{nk}}$
$\ds\leq
\abs{\frac{k}{nk}}
+
\abs{\frac{-n}{nk}}$
$ \ds= \frac{1}{n} + \frac{1}{k}$
$ \ds \lt \frac{\vre}{2} + \frac{\vre}{2}$
$ \ds= \vre . \; \blacksquare$