Mathematical Analysis
Lecture 18
9.4 Interchange of limits
Can we always interchange
limit operations? 🤔
For example
$0=$
$\ds \lim_{n\to\infty}
\left(
\lim_{k\to\infty}
\frac{n}{n + k}
\right)$
$\ds \neq $
$\ds \lim_{k\to\infty}
\left(
\lim_{n\to\infty}
\frac{n}{n + k}
\right)$
$=1$
Are these limits equal?
Of course, no!
9.4 Interchange of limits
In general, we would like to find conditions on the sequence $\{ f_n \}_{n=1}^\infty$ so that the equation below holds:
$\ds \lim_{k \to \infty} \Bigl( \lim_{n \to \infty} f_n(x_k) \Bigr) \overset{?}{=} \lim_{n \to \infty} \Bigl( \lim_{k \to \infty} f_n(x_k) \Bigr)$
Example 9.4.1.
Define $f_n \colon [0,1] \to \R$ as \begin{equation*} f_n(x) \coloneqq \begin{cases} 1-nx & \text{if } x \lt \dfrac{1}{n},\\ 0 & \text{if } x \geq \dfrac{1}{n}. \end{cases} \end{equation*}
Example 9.4.1.
Define $f_n \colon [0,1] \to \R$ as $ f_n(x) \coloneqq \begin{cases} 1-nx & \text{if } x \lt \frac{1}{n},\\ 0 & \text{if } x \geq \frac{1}{n}. \end{cases}$
Example 9.4.1.
Define $f_n \colon [0,1] \to \R$ as $ f_n(x) \coloneqq \begin{cases} 1-nx & \text{if } x \lt \frac{1}{n},\\ 0 & \text{if } x \geq \frac{1}{n}. \end{cases}$
Note that $f_n$ is continuous.
Consider a fix $x \in (0,1].$
If $n \geq \dfrac{1}{x},$
then $x \geq \dfrac{1}{n}.$
Thus for $n \geq \dfrac{1}{x},$
we have that $f_n(x) = 0,$
and so
\begin{equation*}
\lim_{n \to \infty} f_n(x) = 0.
\end{equation*}
Now if $x=0,$ then $\ds \lim_{n \to \infty} f_n(0)$ $\ds = \lim_{n \to \infty} 1 $ $ = 1.$
Example 9.4.1.
Define $f_n \colon [0,1] \to \R$ as $ f_n(x) \coloneqq \begin{cases} 1-nx & \text{if } x \lt \frac{1}{n},\\ 0 & \text{if } x \geq \frac{1}{n}. \end{cases}$
Thus $f_n$ converges pointwise to the function $f \colon [0,1] \to \R$ defined by \begin{equation*} f(x) \coloneqq \begin{cases} 1 & \text{if } x = 0,\\ 0 & \text{if } x > 0. \end{cases} \end{equation*} Observe that the function $f$ is not continuous at 0.
9.4.1 Continuity of the limit
Theorem 9.4.1. Let $\{ f_n \}$ be a sequence of continuous functions $f_n \colon S \to \R$ converging uniformly to $f \colon S \to \R$. Then $f$ is continuous.
9.4.1 Continuity of the limit
Theorem 9.4.1. Let $\{ f_n \}$ be a sequence of continuous functions $f_n \colon S \to \R$ converging uniformly to $f \colon S \to \R$. Then $f$ is continuous.
Proof. Fix $c\in S$ and let $\epsilon\gt 0.$ Choose $N$ so that
$\ds \abs{f_N(x) - f(x)}\lt \frac{\epsilon}{3}\;$ for all $\;x\in S.$
Since $f_N$ is continuous, there exists a $\delta \gt 0 $ such that
$\ds \abs{f_N(x) - f_N(c)}\lt \frac{\epsilon}{3}\;$ is true whenever $\abs{x-c}\lt \delta.$
9.4.1 Continuity of the limit
Theorem 9.4.1. Let $\{ f_n \}$ be a sequence of continuous functions $f_n \colon S \to \R$ converging uniformly to $f \colon S \to \R$. Then $f$ is continuous.
Proof.
$\ds \abs{f_N(x) - f(x)}\lt \frac{\epsilon}{3}\;$ for all $\;x\in S.$
$\ds \abs{f_N(x) - f_N(c)}\lt \frac{\epsilon}{3}\;$ is true whenever $\abs{x-c}\lt \delta.$
$\Ra \abs{f(x)-f(c)} $
$= \abs{f(x)-f_N(x)+f_N(x)-f_N(c)+f_N(c)-f(c)}\quad $
$\leq \abs{f(x)-f_N(x)}+ \abs{f_N(x)-f_N(c)}+ \abs{f_N(c)-f(c)}$
$ \ds\,\quad \lt \frac{\epsilon}{3} + \frac{\epsilon}{3} + \frac{\epsilon}{3} $ $ \ds = \epsilon. \;$ Hence, $f$ is continuous. $ \;\bs$
Example 9.4.2.
Define $f_n \colon [0,1] \to \R$ as \begin{equation*} f_n(x) \coloneqq \begin{cases} n^2x & \text{if } 0\leq x\leq \dfrac{1}{n},\\ -n^2\left(x-\dfrac{2}{n}\right) & \text{if } \dfrac{1}{n} \leq x \leq \dfrac{2}{n},\\ 0 & \text{if } \dfrac{2}{n}\leq x \leq 1. \end{cases} \end{equation*}
Example 9.4.2.
Define $f_n \colon [0,1] \to \R$ as $ f_n(x) \coloneqq \begin{cases} n^2x & \text{if } 0\leq x\leq \frac{1}{n},\\ -n^2\left(x-\frac{2}{n}\right) & \text{if } \frac{1}{n} \leq x \leq \frac{2}{n},\\ 0 & \text{if } \frac{2}{n}\leq x \leq 1. \end{cases}$
Example 9.4.2.
Since each of the functions $f_n$ is continuous on $[0,1]$, then $f$ Riemann integrable. For $n\geq 2$, using the FTC,
$\ds \int_0^1 f_n $
$\ds =
\int_0^{1/n} n^2x\,dx $
$\ds
+ \int_{1/n}^{2/n} -n^2\left(x-\frac{2}{n}\right) dx$
$\ds =
\frac{1}{2} + \frac{1}{2}$
$\ds =
1. \qquad \qquad \quad \;\;\;$
Now to compute $\lim f_n$ fix an $x\in[0,1].$ For $n\geq \dfrac{2}{x}$, we have $x \geq \dfrac{2}{n}$ and so $f_n(x) = 0$. Therefore, $\lim f_n = 0.$
Example 9.4.2.
Thus we have
$\ds 1 = $ $\ds \lim_{n\to\infty} \int_0^1 f_n $ $\ds \not= \int_0^1 \left( \lim_{n\to\infty} f_n\right)$ $\ds=\int_0^1 0$ $\ds =0$
Example 9.4.3.
Consider the functions $$f_n(x):= 2n x e^{-n x^2} \,\text{ for } \,x\in [0,1].$$
Example 9.4.3.
$f_n(x):= 2n x e^{-n x^2}$ for $x\in [0,1].$
Example 9.4.3.
$f_n(x):= 2n x e^{-n x^2}$ for $x\in [0,1].$
Since $f_n = F'_n$ where $F_n(x):= -e^{-nx^2} ,$ then
$\ds \int_0^1 f_n $ $ = F_n(1)- F_n(0)$ $ = 1- e^{-n}.$
We also have that $f(x)= \ds \lim_{n\to \infty} f_n = 0$ for all $x\in[0,1]$. Hence
$0=$ $\ds \int_0^1 f $ $\ds \,\neq \,$ $\ds \lim_{n\to \infty} \int_0^1 f_n$ $\ds = \lim_{n\to \infty} \left(1 - e^{-n}\right)$ $=1.$
9.4.2 Integral of the limit
Theorem 9.4.2. Let $\{ f_n \}$ be a sequence of Riemann integrable functions $f_n \colon [a,b] \to \R$ converging uniformly to $f \colon [a,b] \to \R.$ Then $f$ is Riemann integrable, and \begin{equation*} \int_a^b f = \lim_{n\to\infty} \int_a^b f_n . \end{equation*}
👀 Complementary reading 📖
Example 9.4.4.
Suppose we wish to compute \begin{equation*} \lim_{n\to\infty} \int_0^1 \frac{nx+ \sin(nx^2)}{n} \,dx . \end{equation*}
Using Theorem 9.4.2, we have
$\ds \lim_{n\to\infty} \int_0^1 \frac{nx+ \sin(nx^2)}{n} \,dx$ $\ds = \int_0^1 x \,dx$ $\ds =\frac{1}{2}.$
Example 9.4.5.
If convergence is only pointwise, the limit need not even be Riemann integrable. On $[0,1]$ define \begin{equation*} f_n(x) \coloneqq \begin{cases} 1 & \text{if } x = \dfrac{p}{q} \text{ in lowest terms and } q \leq n, \\ 0 & \text{otherwise.} \end{cases} \end{equation*}
👀 Complementary reading 📖
Example 9.4.6.
If the convergence is only pointwise, the limit of bounded functions is not even necessarily bounded. Define $f_n \colon [0,1] \to \R$ by \begin{equation*} f_n(x) \coloneqq \begin{cases} 0 & \text{if } x \lt \dfrac{1}{n},\\ \dfrac{1}{x} & \text{else.} \end{cases} \end{equation*}
👀 Complementary reading 📖
Example 9.4.7.
Now we are going to consider derivatives of sequences of functions.
Let $\ds f_n(x) \coloneqq \frac{\sin(nx)}{n}$. Then $f_n$ converges uniformly to $0.$
Example 9.4.7.
Let $\ds f_n(x) \coloneqq \frac{\sin(nx)}{n}$. Then $f_n$ converges uniformly to $0.$
Example 9.4.7.
Let $\ds f_n(x) \coloneqq \frac{\sin(nx)}{n}$. Then $f_n$ converges uniformly to $0.$
The derivative of the limit is 0. But $f_n'(x) = \cos(nx)$, which does not converge even pointwise, for example consider $$f_n'(\pi) = {(-1)}^n.$$
Also note that $f_n'(0) = 1$ for all $n$, which converges, but not to $0$.
Example 9.4.8.
Let $\ds f_n(x) \coloneqq \dfrac{1}{1+nx^2}$. If $x \not= 0$, then $$\lim_{n \to \infty} f_n(x) = 0,$$ but $\lim_{n \to \infty} f_n(0) = 1$.
Thus, $\{ f_n \}_{n=1}^\infty$ converges pointwise to a function that is not continuous at $0$.
Example 9.4.8.
Let $\ds f_n(x) \coloneqq \dfrac{1}{1+nx^2}$. If $x \not= 0$, then $\lim_{n \to \infty} f_n(x) = 0,$ but $\lim_{n \to \infty} f_n(0) = 1$.
Thus, $\{ f_n \}_{n=1}^\infty$ converges pointwise to a function that is not continuous at $0$.
In this case we have that $\ds f_n'(x)$ $\ds = \frac{-2 n x}{\left(1+ n x^2\right)^2} .$
For every $x,$ $\lim_{n\to\infty} f_n'(x) = 0,$ then the derivatives converge pointwise to $0.$ However, the convergence is not uniform on any interval containing $0$.
The limit of $f_n$ is not differentiable at $0$. In fact, it is not even continuous at $0$.
Example 9.4.8.
1. If $x \not= 0$, then $\lim_{n \to \infty} f_n(x) = 0,$ but $\lim_{n \to \infty} f_n(0) = 1$.
2. For every $x$, $\lim_{n\to\infty} f_n'(x) = 0$. The convergence is not uniform on any interval containing $0$.
Example 9.4.8.
Thus we have that
$\ds 0=$ $\ds \lim_{n\to \infty} f_n'(0)$ $\ds \neq f'(0)$ $\ds = \left(\lim_{n\to \infty} f_n(0)\right)'$ $\ds =1.$
9.4.3 Derivative of the limit
Theorem 9.4.3. Let $I$ be a bounded interval and let $f_n \colon I \to \R$ be continuously differentiable functions. Suppose $\{ f_n' \}$ converges uniformly to $g \colon I \to \R,$ and suppose $\bigl\{ f_n(c) \bigr\}_{n=1}^\infty$ is a convergent sequence for some $c \in I.$ Then $\{ f_n \}$ converges uniformly to a continuously differentiable function $f \colon I \to \R$, and $f' = g.$
👀 Complementary reading 📖
Fourier series (Not examinable)
The Fourier series of a real function $f$ defined on the interval $(-p,p)$ is given by
$ \ds f(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty}\left(a_n\,\cos \left(\frac{n\, \pi}{p}x\right)+b_n\,\sin \left(\frac{n\, \pi}{p}x\right) \right), $
where
$\ds \begin{eqnarray*} a_0&=&\frac{1}{p}\int_{-p}^pf(x)\,dx,\\ a_n&=&\frac{1}{p}\int_{-p}^pf(x)\,\cos \left(\frac{n\, \pi}{p}x\right)\,dx,\\ b_n&=&\frac{1}{p}\int_{-p}^pf(x)\,\sin \left(\frac{n\, \pi}{p}x\right)\,dx. \end{eqnarray*} $
The Fourier series is named in honor of Jean Baptiste Joseph Fourier (1768-1830).
Fourier series (Not examinable)
Example: Consider the function defined by $f(x)=x+\pi$ for $-\pi < x < \pi $ and $f(x)=f(x+2\pi)$ for $-\infty < x < \infty$. Its Fourier series expansion is \[ f(x)=\pi+2\sum_{n=1}^{\infty}\frac{\left(-1\right)^{n+1}}{n}\sin (n\,x). \]
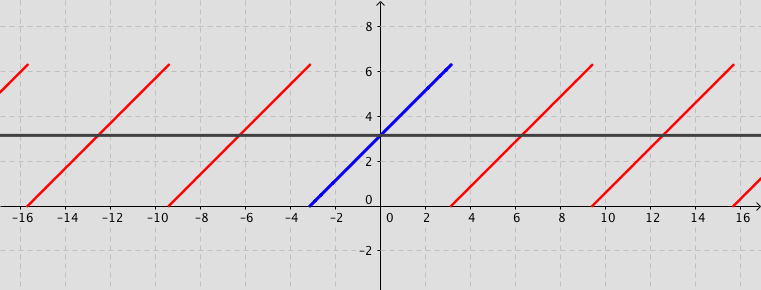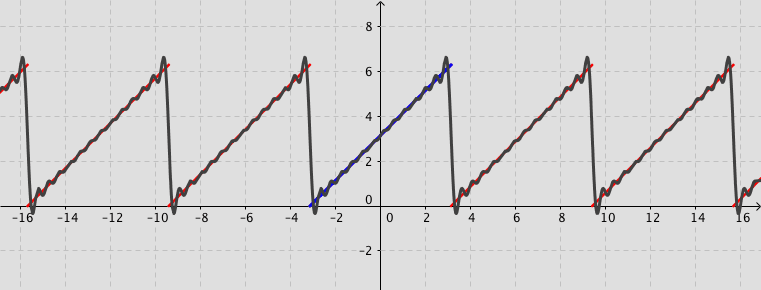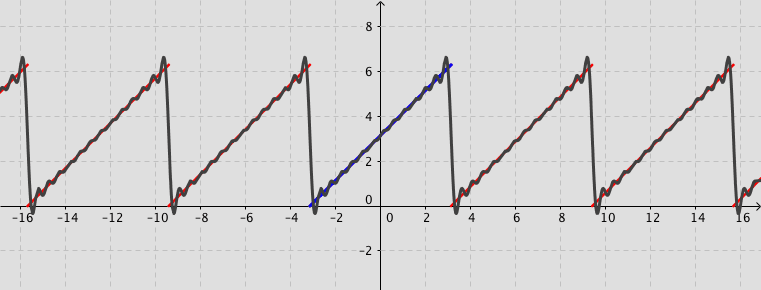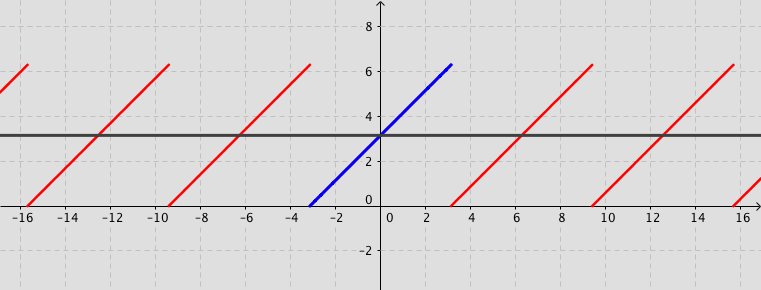
Fourier series (Not examinable)
The square wave
Fourier series (Not examinable)
|
The square wave Fourier applets by: Jez Swanson |
|