Mathematical Analysis
Summary Week 2
❤️ Support this project ❤️
PatreonSequences
Convergence of sequences

Definition: A sequence $\{ x_n \}$ is said to converge to a number $x \in \R$ if for every $\epsilon > 0$, there exists an $M \in \N$ such that $\abs{x_n - x} < \epsilon$ for all $n \geq M$. The number $x$ is said to be the limit of $\{ x_n \}$. We write \begin{equation*} \lim_{n\to \infty} x_n := x . \end{equation*}
Sequences
Convergence of sequences
Sequences
Bounded & Monotone
Theorem: A monotone sequence $\{ x_n \}$ is bounded if and only if it is convergent.
Sequences
Bounded & Monotone
| Increasing | Decreasing |
|---|
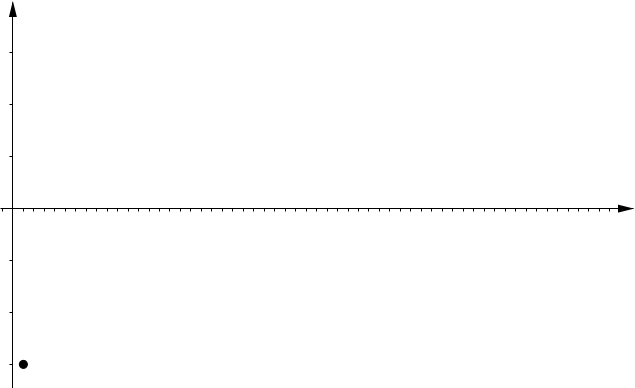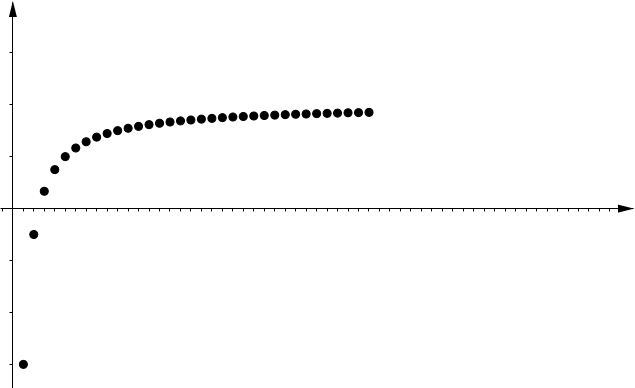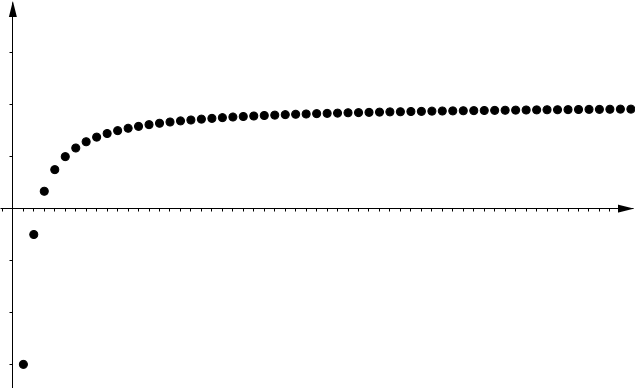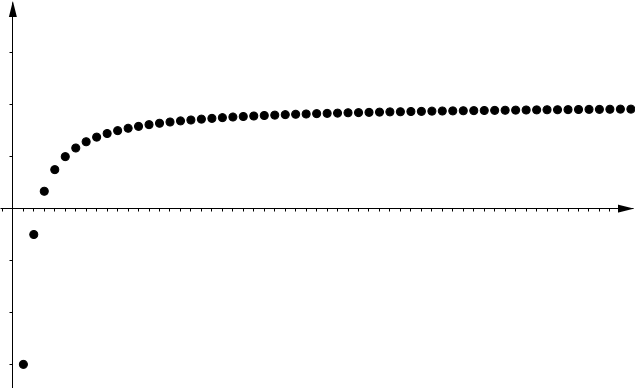
|
|
| $\displaystyle \lim_{n\to \infty} x_n = \sup \{ x_n : n \in \N \}$ | $\displaystyle \lim_{n\to \infty} x_n = \inf \{ x_n : n \in \N \}$ |
Sequences
Squeeze Theorem

Sequences
Squeeze Theorem
|
Theorem: Let $\{ a_n \}$, $\{ b_n \}$, and $\{ x_n \}$ be sequences such that \begin{equation*} a_n \leq x_n \leq b_n \quad \text{for all } n \in \N. \end{equation*} Suppose $\{ a_n \}$ and $\{ b_n \}$ converge and \begin{equation*} \lim_{n\to \infty} a_n = \lim_{n\to \infty} b_n . \end{equation*} Then $\{ x_n \}$ converges and \begin{equation*} \lim_{n\to \infty} x_n = \lim_{n\to \infty} a_n = \lim_{n\to \infty} b_n . \end{equation*} |

|
|---|
Sequences
Algebraic properties
Theorem: Let $\{ x_n \}$ and $\{ y_n \}$ be convergent sequences.
- The sequence $\{ z_n \}$, where $z_n := x_n \pm y_n$, converges and \begin{equation*} \lim_{n \to \infty} (x_n \pm y_n) = \lim_{n \to \infty} z_n = \lim_{n \to \infty} x_n \pm \lim_{n \to \infty} y_n . \end{equation*}
- The sequence $\{ z_n \}$, where $z_n := x_n y_n$, converges and \begin{equation*} \lim_{n \to \infty} (x_n y_n) = \lim_{n \to \infty} z_n = \left( \lim_{n \to \infty} x_n \right) \left( \lim_{n \to \infty} y_n \right) . \end{equation*}
- If $\lim\, y_n \not= 0$ and $y_n \not= 0$ for all $n \in \N$, then the sequence $\{ z_n \}$, where $z_n := \dfrac{x_n}{y_n}$, converges and \begin{equation*} \lim_{n \to \infty} \frac{x_n}{y_n} = \lim_{n \to \infty} z_n = %\frac{\lim_{n \to \infty} x_n}{\lim_{n \to \infty} y_n} . \frac{\lim\, x_n}{\lim\, y_n} . \end{equation*}
Sequences
Some convergence tests
Theorem: Let $\{ x_n \}$ be a sequence. Suppose there is an $x \in \R$ and a convergent sequence $\{ a_n \}$ such that \begin{equation*} \lim_{n\to\infty} a_n = 0 \quad \text{ and } \quad \abs{x_n - x} \leq a_n \quad \text{for all $n \in \N$.} \end{equation*} Then $\{ x_n \}$ converges and $\lim\, x_n = x$.
Theorem: Let $c > 0$.
- If $c \lt 1$, then $\lim_{n\to\infty} c^n = 0.$
- If $c \gt 1$, then $\{ c^n \}$ is unbounded.
Sequences
Some convergence tests
Theorem (Ratio test for sequences): Let $\{ x_n \}$ be a sequence such that $x_n \not= 0$ for all $n$ and such that the limit \begin{equation*} L := \lim_{n\to\infty} \frac{\abs{x_{n+1}}}{\abs{x_n}} \qquad \text{exists.} \end{equation*}
- If $L < 1$, then $\{ x_n \}$ converges and $\lim\, x_n = 0$.
- If $L > 1$, then $\{ x_n \}$ is unbounded (hence diverges).
Sequences
Upper & lower limits
Definition: Let $\{ x_n \}$ be a bounded sequence. Define the sequences $\{ a_n \}$ and $\{ b_n \}$ by $a_n := \sup \{ x_k : k \geq n \}$ and $b_n := \inf \{ x_k : k \geq n \}$. Define, if the limits exist, \begin{align*} \limsup_{n \to \infty} \, x_n & := \lim_{n \to \infty} a_n , \\ \liminf_{n \to \infty} \, x_n & := \lim_{n \to \infty} b_n . \end{align*}
Sequences
Upper & lower limits

$x_n$ is bounded.
Sequences
Upper & lower limits
|
Theorem: Let $\{ x_n \}$ be a bounded sequence. Let $a_n$ and $b_n$ be as in the definition above.
|

|
|---|
Sequences
Upper & lower limits

$x_n$ is bounded and convergent.
Sequences
Upper & lower limits
|
Theorem: Let $\{ x_n \}$ be a bounded sequence. Then $\{ x_n \}$ converges if and only if \begin{equation*} \liminf_{n\to \infty} \, x_n = \limsup_{n\to \infty} \, x_n. \end{equation*} Furthermore, if $\{ x_n \}$ converges, then \begin{equation*} \lim_{n\to \infty} x_n = \liminf_{n\to \infty} \, x_n = \limsup_{n\to \infty} \, x_n. \end{equation*} |

|
|---|
Sequences
Bolzano-Weierstrass Theorem
Theorem: Suppose a sequence $\{ x_n \}$ of real numbers is bounded. Then there exists a convergent subsequence $\{ x_{n_i} \}$.
Sequences
Cauchy sequences

if for every $\epsilon > 0$ there exists an $M \in \N$ such that for all $n \geq M$ and all $k \geq M$,
we have $\abs{x_n - x_k} < \epsilon .$
Sequences
Cauchy sequences
|
Theorem: A Cauchy sequence is bounded. Theorem: A sequence of real numbers is Cauchy if and only if it converges. |

|
|---|