Mathematical Analysis
Summary Week 3
❤️ Support this project ❤️
PatreonSeries
Definition: Given a sequence $\{ x_n \}$,
we write the formal object
\begin{equation*}
\sum_{n=1}^\infty x_n
\qquad
\text{or sometimes just}
\qquad
\sum x_n
\end{equation*}
and call it a series.
A series
converges if the sequence $\{ s_k \}$
defined by
$s_k := \displaystyle\sum_{n=1}^k x_n = x_1 + x_2 + \cdots + x_k ,$
converges.
The numbers $s_k$ are called
partial sums.
If $x := \lim\, s_k$, we write
\begin{equation*}
\sum_{n=1}^\infty x_n = x .
\end{equation*}
Series
Sequence of Partial sums
Series
Geometric series
Theorem: Suppose $-1 < r < 1$. Then the geometric series $\sum_{n=0}^\infty r^n$ converges, and \begin{equation*} \sum_{n=0}^\infty r^n = \frac{1}{1-r} . \end{equation*}
Series
Geometric series $\sum_{n=0}^\infty r^n = \frac{1}{1-r}$
Series
Cauchy series
Definition: A series $\sum x_n$ is said to be Cauchy or a Cauchy series if the sequence of partial sums $\{ s_n \}$ is a Cauchy sequence.
Series
Basic Properties
Theorem: Let $\sum x_n$ be a convergent series. Then the sequence $\{ x_n \}$ is convergent and \begin{equation*} \lim_{n\to\infty} x_n = 0. \end{equation*}
Series
Basic properties: $\sum x_n$ convergent $\implies \lim x_n =0$
Series
Basic properties: But $\lim x_n =0$ does not implies $\sum x_n$ convergent
Series
Basic Properties
Theorem (Linearity of series): Let $\alpha \in \R$ and $\sum x_n$ and $\sum y_n$ be convergent series. Then
- $\sum \alpha x_n$ is a convergent series and \begin{equation*} \qquad\qquad\qquad\qquad\qquad\sum_{n=1}^\infty \alpha x_n = \alpha \sum_{n=1}^\infty x_n . \end{equation*}
- $\sum ( x_n + y_n )$ is a convergent series and \begin{equation*} \qquad\qquad\qquad\qquad\qquad\sum_{n=1}^\infty ( x_n + y_n ) = \left( \sum_{n=1}^\infty x_n \right) + \left( \sum_{n=1}^\infty y_n \right) . \end{equation*}
Series
Absolute convergence
Theorem: If $x_n \geq 0$ for all $n$, then $\sum x_n$ converges if and only if the sequence of partial sums is bounded above.
Definition: A series $\sum x_n$ converges absolutely if the series $\sum \abs{x_n}$ converges. If a series converges, but does not converge absolutely, we say it is conditionally convergent.
Theorem: If the series $\sum x_n$ converges absolutely, then it converges.
Series
Absolute convergence
Series
Convergence tests
Theorem (Comparison test): Let $\sum x_n$ and $\sum y_n$ be series such that $0 \leq x_n \leq y_n$ for all $n \in \N$.
- If $\sum y_n$ converges, then so does $\sum x_n$.
- If $\sum x_n$ diverges, then so does $\sum y_n$.
Theorem (Ratio test): Let $\sum x_n$ be a series, $x_n \not= 0$ for all $n$, and such that \begin{equation*} L := \lim_{n\to\infty} \frac{\abs{x_{n+1}}}{\abs{x_n}} \qquad \text{exists.} \end{equation*}
- If $L \lt 1$, then $\sum x_n$ converges absolutely.
- If $L \gt 1$, then $\sum x_n$ diverges.
Series
Ratio test
Series
Convergence tests
Theorem ($p$-test): For $p \in \R$, the series \begin{equation*} \sum_{n=1}^\infty \frac{1}{n^p} \end{equation*} converges if and only if $p \gt 1$.
Series
Convergence test for $\sum_{n=1}^\infty \frac{1}{n^p}$
Series
Fun fact! 🧐
|
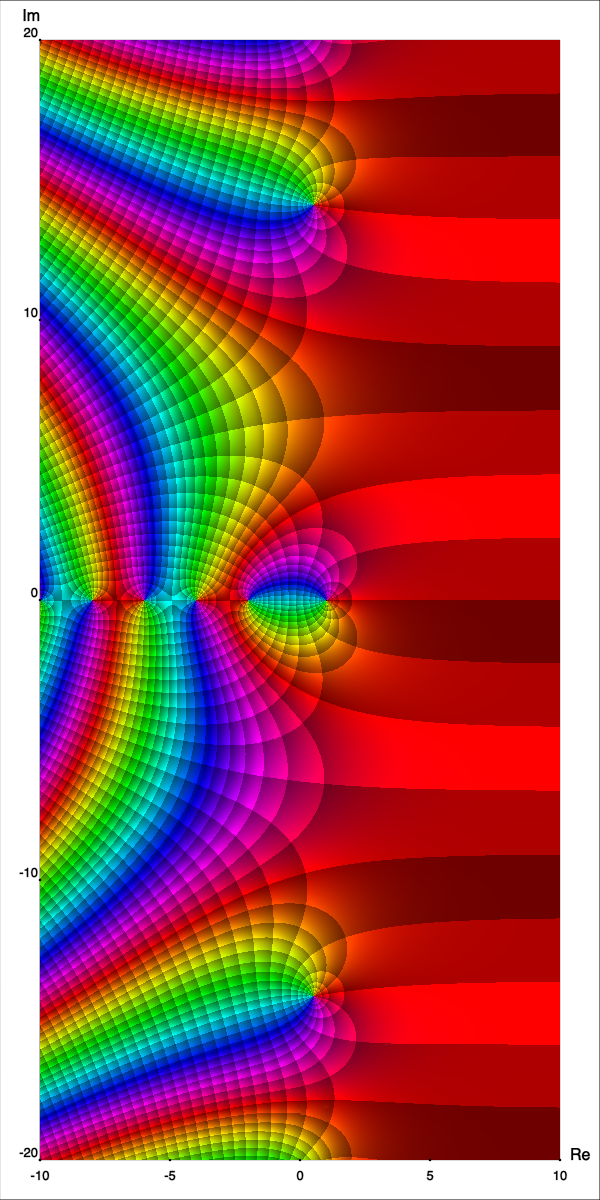
The function $$\zeta(s) := \sum_{n=1}^{\infty}\frac{1}{n^s}$$ is the famous Riemann Zeta function. One of the most important open problems in mathematics, the Riemann hypothesis, is concerned with the zeros of $\zeta(s)$, when $s \in \C$. It encodes fundamental information on the distribution of prime numbers. |
|
|---|
Series
Convergence tests
Theorem (Root test): Let $\sum x_n$ be a series and let $ \displaystyle L := \limsup_{n\to\infty} \, {\abs{x_n}}^{1/n} . $
- If $L \lt 1$, then $\sum x_n$ converges absolutely.
- If $L \gt 1$, then $\sum x_n$ diverges.
Theorem (Alternating series): Let $\{ x_n \}$ be a monotone decreasing sequence of positive real numbers such that $\lim\, x_n = 0$. Then \begin{equation*} \sum_{n=1}^\infty {(-1)}^n x_n \end{equation*} converges.