MATH3401
Complex Analysis
Lecture 1
Complex Analysis
- \(e^{i\pi} = -1\)
- \(\ds \int_0^{\infty}\dfrac{\sin x}{x} dx=\dfrac{\pi}{2}\)
- Recall that \(\ds \int_0^1\dfrac{dx}{x}= \ds \lim_{\varepsilon \ra 0^+}\int_{\varepsilon}^1\dfrac{dx}{x}\) diverges
- And \(\ds \int_1^{\infty}\dfrac{dx}{x}= \ds \lim_{M \ra \infty}\int_{1}^{M}\dfrac{dx}{x}\) also diverges
Complex Analysis
Methods for contour integrals
Complex Analysis
Fluid flow
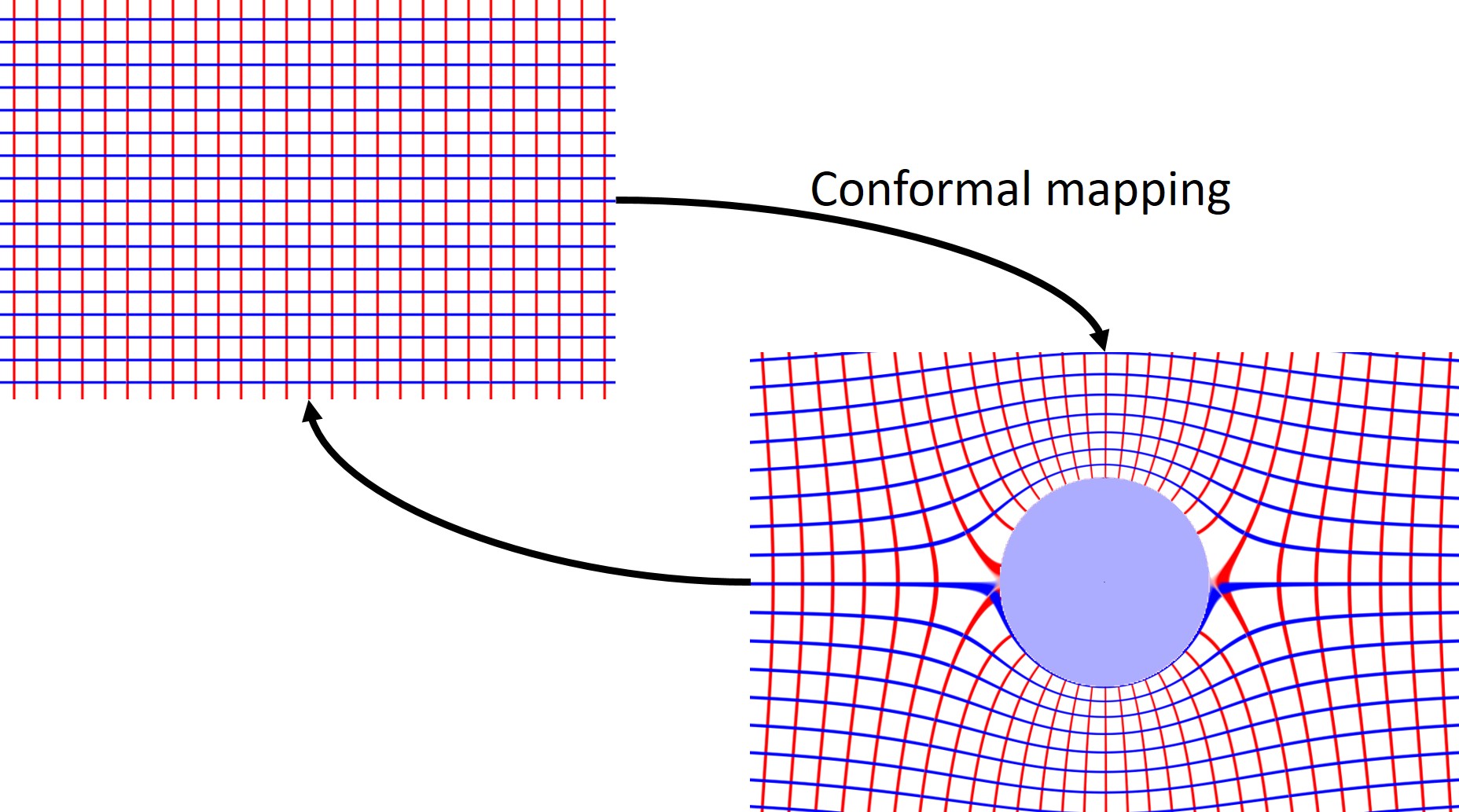
Complex Analysis
Air flow
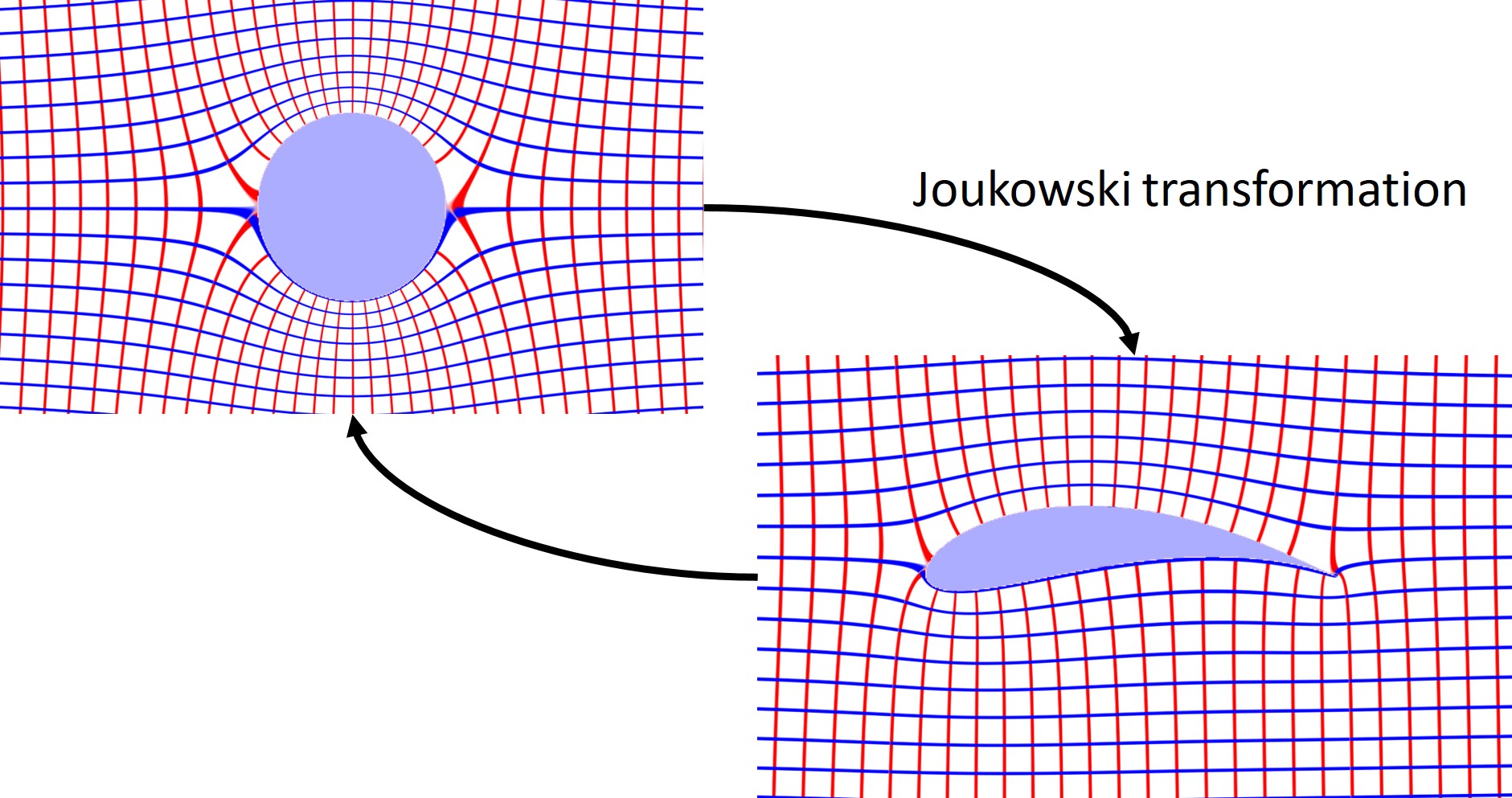
Complex Analysis
Series
\(\text{I.} \;\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots =\frac{\pi^2}{6}\)
\(\text{II.} \;\frac{1}{1^2}-\frac{1}{2^2}+\frac{1}{3^2}-\cdots =\frac{\pi^2}{12}\)
\(\text{III.} \;{\small \ds \sum_{k=1}^{\infty} \frac{1}{1+4k^2\pi^2}=\frac{1}{2}\left( \frac{1}{e-1}-\frac{1}{2}\right)}\)
Complex Analysis
Series
\(\zeta(s) = \ds \sum_{n=1}^{\infty}\frac{1}{n^s}= \ds \prod_{p\;\text{prime}}(1-p^{-s})^{-1}\)
\(\zeta\) is the Riemann zeta function.
Complex Analysis
Riemann hypothesis
\(\zeta(s) = \ds \sum_{n=1}^{\infty}\frac{1}{n^s}= \ds \prod_{p\;\text{prime}}(1-p^{-s})^{-1}\)
\(\zeta\) has infinitely many non-trivial zeros and they all lie on the line \(\Re(s)=\dfrac{1}{2}\)
Complex Analysis
Riemann hypothesis
\(\zeta(s) = \ds \sum_{n=1}^{\infty}\frac{1}{n^s}= \ds \prod_{p\;\text{prime}}(1-p^{-s})^{-1}\)
Only makes sense for \(\Re(s)>1\):
Need to extend \(\zeta\) to \(\C\) via analytic continuation.
Complex Analysis
Riemann hypothesis
\(\zeta(s) = \ds \sum_{n=1}^{\infty}\frac{1}{n^s}= \ds \prod_{p\;\text{prime}}(1-p^{-s})^{-1}\)
Trivial zeros are \(-2, -4, -6, \cdots\)
Millenium problem!