Gallery
Domain Coloring Gallery
HSL standard scheme
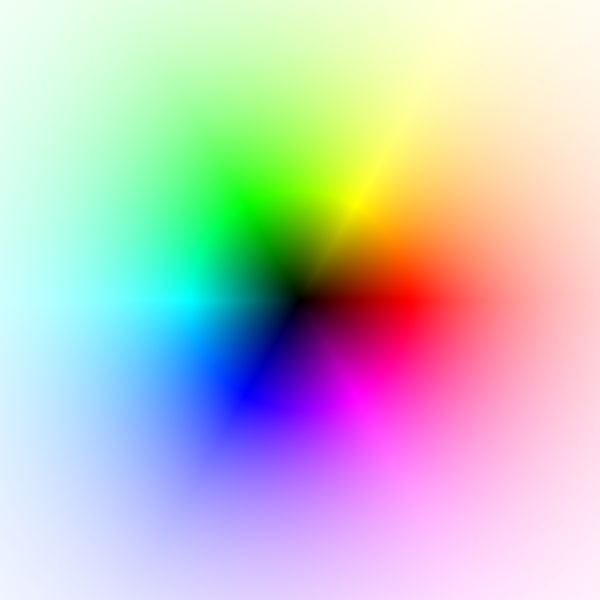
$z$
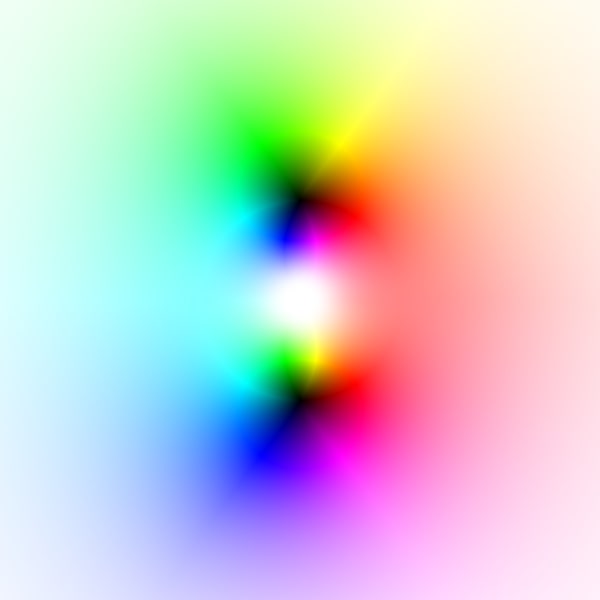
$z+\dfrac{1}{z}$

$\dfrac{1}{z}$

$z^{1/2}$

$z^{6}+1$

$\dfrac{z-1}{z^2+z+1}$
HSB scheme
Enhanced phase portraits for the function $f(z)=\dfrac{z-1}{z^2+z+1}.$
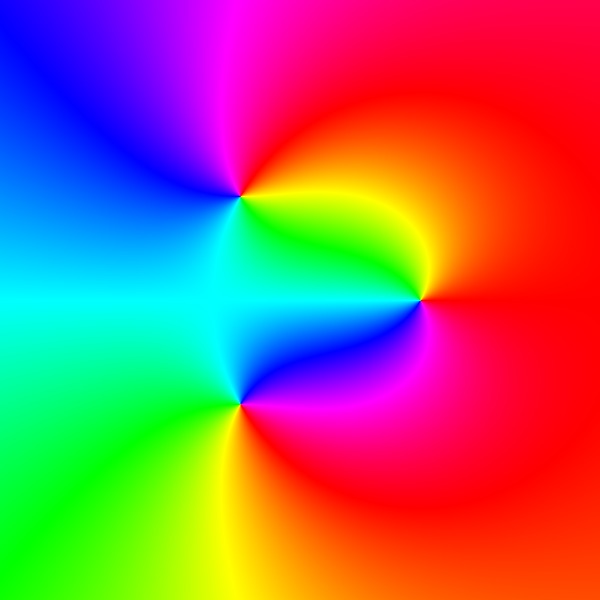
Simple phase portrait.

Phase contour lines.

Modulus contour lines.

Contour lines of modulus and phase.
Branches
$f(z)=z^{1/2}$

Branch 1

Branch 2
$f(z)=\sqrt{1-z^{2}}$
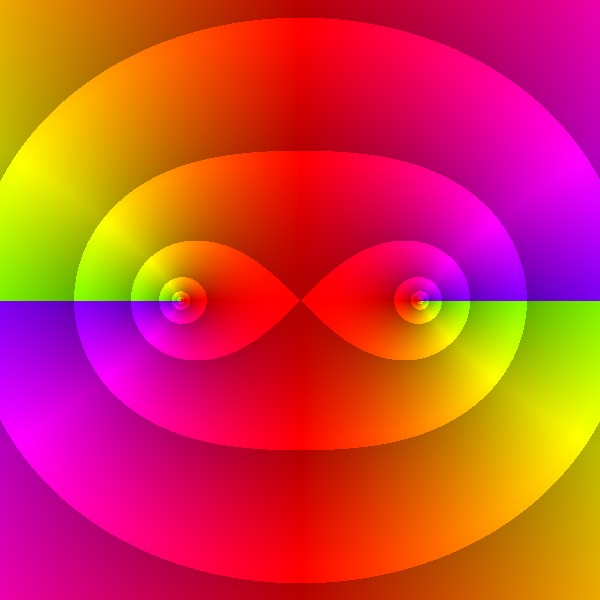
Branch 1

Branch 2
$f(z)=\dfrac{1}{\sqrt{1-z^{2}}}$

Branch 1
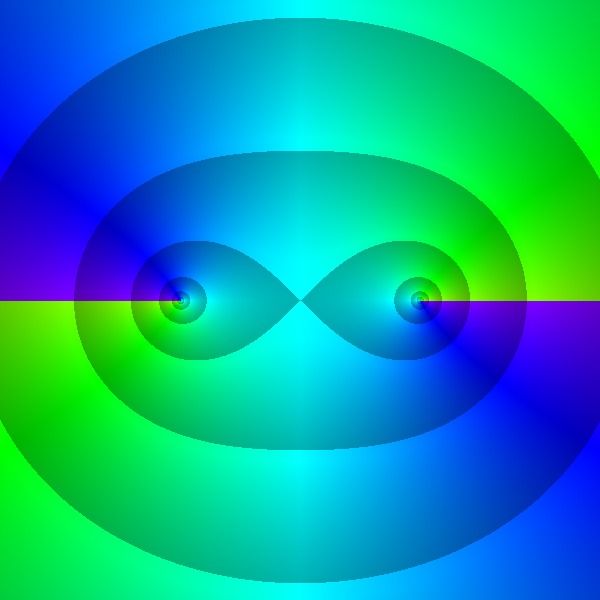
Branch 2
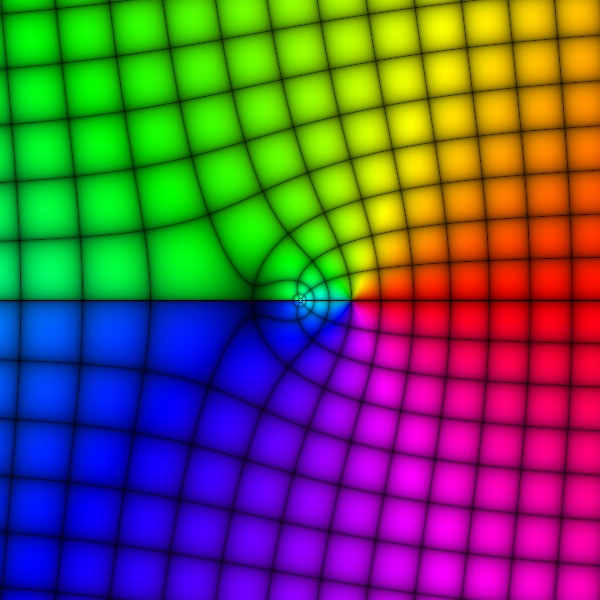
$f(z)=\log z$

Branch -1

Principal branch

Branch 1
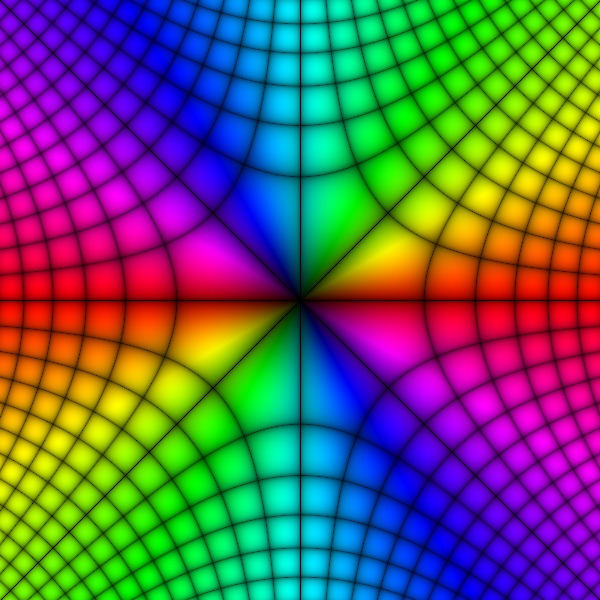
$f(z)=\arctan z$

Branch -1

Principal branch

Branch 1
Singularities
Pole of order 1

$\dfrac{1-\cosh z}{z^3}$
Pole of order 2

$\dfrac{\exp (2z)}{(z-1)^2}$
Pole of order 3

$\dfrac{\sinh z}{z^4}$
Removable singularities

$\dfrac{\sin\left(z\right)}{z}$

$\dfrac{1-\cos z}{z^2}$

$\dfrac{z}{e^z-1}$
Essential singularities

$\exp\left(\dfrac{1}{z}\right)$

$(z-1)\cos\left(\dfrac{1}{z}\right)$

$z \sin\left(\dfrac{1}{iz}\right)$
Level curves of real and imaginary components
$z^2$

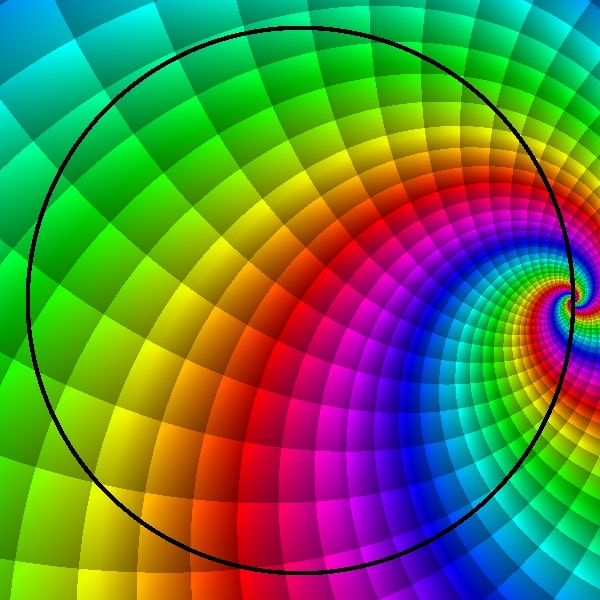
$\log\left(\frac{z-1}{z+1}\right)$

$z+\frac{1}{z}$
$z+\log\left(z\right)/\pi$
Hypergeometric functions
$$_2F_1\left(a,b;c;z\right)=\sum_{n=0}^{\infty}\frac{(a)_n (b)_n}{(c)_n}\frac{z^n}{n!}$$

$_2F_1\left(1,\frac{3}{4};\frac{1}{2};z\right)$

$_2F_1\left(1-i,\frac{3}{4}i;-\frac{1}{2}i;z^2\right)$
Special cases

$z\cdot\, _2F_1\left(1,1;2;-z\right)$

$\log(1+z)$

$_2F_1\left(2-3i,b;b;z\right)$ $\,\forall b$
$(1-z)^{-(2-3i)}$

$z\cdot \,_2F_1\left(\frac{1}{2},1;\frac{3}{2};-z^2\right)$

$\arctan(z)$
Miscellaneous

$\dfrac{(1/z)^{18}-(1/z)}{1/z-1}$
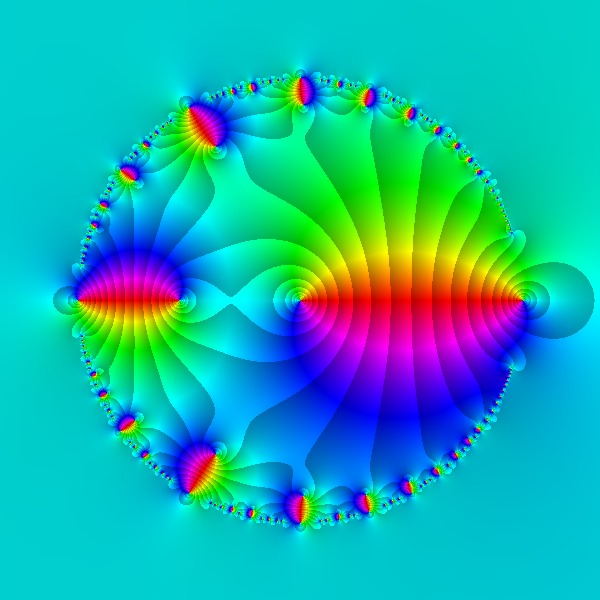
$\displaystyle \sum_{n=1}^{20}\dfrac{z^n}{1-z^n}$

$\sin(1/z^2)$

$\sqrt{1-1/z^2+z^3}$

$\dfrac{(z-2-i)^2(z^2-1)}{z^2+2+i}$

$z^{2/3+i}$

$\displaystyle \sum_{k=1}^{30}z^{ki}$

$\dfrac{z+i}{z-1}$

$e^{1-z^2}-1$

\begin{multline*} 0.926(z+0.073857 z^5\\ +0.0045458 z^9) \end{multline*}

$\dfrac{(2z-2) (z^2+z-i)}{z^4-2+2i}$

\begin{eqnarray*} f(z) &=& z^{1+10i} \cos\left(g(z)\right),\text{ with}\\ g(z) &=& \frac{z-1}{z^{13}+z+1} \end{eqnarray*}

Finite Blaschke product

Atomic Singular Inner Function \({\small \displaystyle \prod_{k=1}^5\exp\left(\dfrac{z+w^k}{z-w^k}\right), w=\exp(2\pi i/5)}\)

Jacobi elliptic function cn$(z, 0.8)$
Different color schemes
Different phase portraits for the function $f(z)=\dfrac{-iz+1}{(-iz)^2-iz+1}.$

Level curves of modulus

Modulus, real and imaginary components

Gradient modulus

Level curves of modulus

Level curves of modulus

Discrete modulus
