The Discrete Fourier Transform
Approximating and drawing closed curves with epicycles
by Juan Carlos Ponce Campuzano, 20/August/2018
Introduction
The Discrete Fourier Transform is defined as \begin{aligned} X_{k}&={\dfrac{1}{N}\sum _{n=0}^{N-1}x_{n}\cdot e^{-i k {\frac {2\pi }{N}}n}}\\ &={ \dfrac{1}{N}\sum _{n=0}^{N-1}x_{n}\left[\cos \left(k{\frac {2\pi }{N}}n\right)-i\, \sin \left({k\frac {2\pi }{N}}n\right)\right],} \end{aligned} where the last expression follows from the first one by Euler's formula. Essentially, it transforms a sequence of $N$ complex numbers $$\displaystyle \mathbf {x} :=x_{0},x_{1},\ldots ,x_{N-1}$$ into another sequence of complex numbers, $$\displaystyle \mathbf {X} :=X_{0},X_{1},\ldots ,X_{N-1}.$$
A few important notes:
- $N =$ number of time samples we have
- $n =$ current sample we're considering $(0 \ldots N-1)$
- $x_n =$ value of the signal at time $n$
- $k =$ current frequency we're considering (0 Hertz up to $N-1$ Hertz)
- $X_k =$ amount of frequency $k$ in the signal (amplitude and phase, a complex number)
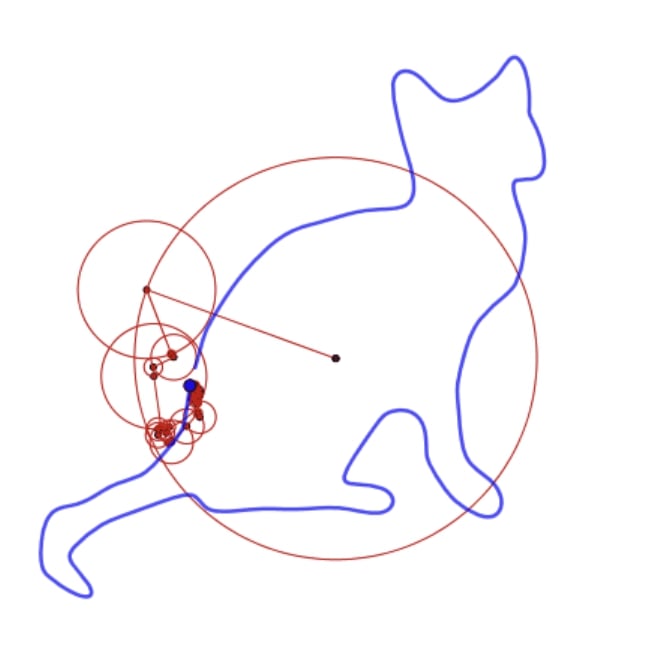
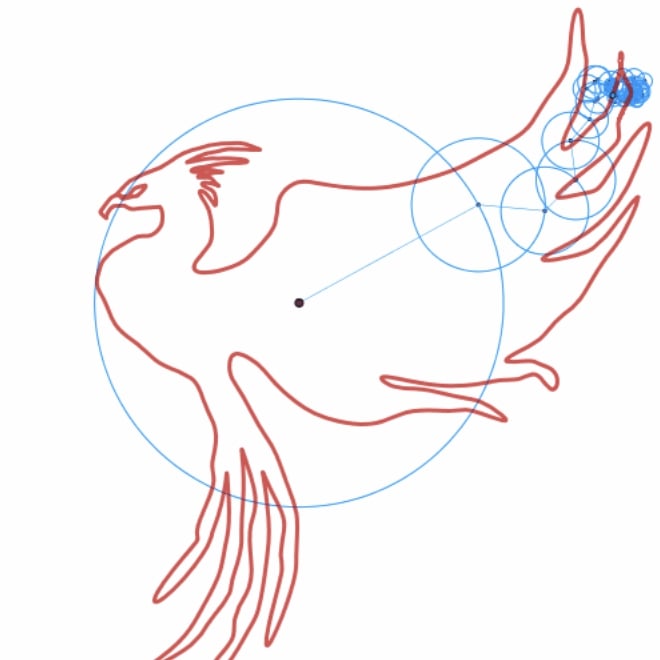
Drawing a T-Rex with epicycles
The animation below with epicycles demonstrates how a simple sum of complex numbers in terms of phases/amplitudes can be nicely visualized as a set of concatenated circles in the complex plane. Each circle represents a Fourier coefficient $X_k$ sorted by amplitude.
Originally the T-Rex curve (signal) is defined with 203 points. After calculating the Fourier coefficient $X_k$, we can easily determine its phase and amplitude for every value of $k$.
Aproximating T-Rex with parametric equations
It is possible to approximate the T-Rex curve. In this case we can use the Fourier coefficients $X_k$ to define the parametric equations: \begin{eqnarray*} x & = \sum_{k=0}^{N-1} \big[ a_k \, \cos\left( k \,t \right) - b_k \, \sin\left( k \,t \right) \big], \\ y & = \sum_{k=0}^{N-1} \big[ b_k \, \cos\left( k \,t \right) + a_k \, \sin\left( k \,t \right) \big] \end{eqnarray*} with $t\in[0, 2\pi)$. The coefficients $a_k$ and $b_k$ are the real and imaginary parts of $X_k$. The expression is obtained using the inverse of the Discrete Fourier Transform: \begin{aligned} x_{n}&=\sum _{k=0}^{N-1}X_{k}\cdot e^{i k {\frac {2\pi }{N}}n}\\ &= \sum _{k=0}^{N-1}x_{n}\left[\cos \left(k{\frac {2\pi }{N}}n\right)+i\,\sin \left({k\frac {2\pi }{N}}n\right)\right]. \end{aligned}
The method to create the system of epicycles to draw a T-rex works also for any possible periodic signal.
Further details
For more details about how this method works and how to implement it in p5js, see:
How it works?- Tracing closed curves with epicycles: A fun application of the discrete Fourier transform.
- Trigonometric intepolation using the Discrete Fourier Transform.
Finally, if you find this content useful, please consider supporting my work using the links below.
∞ Thanks!
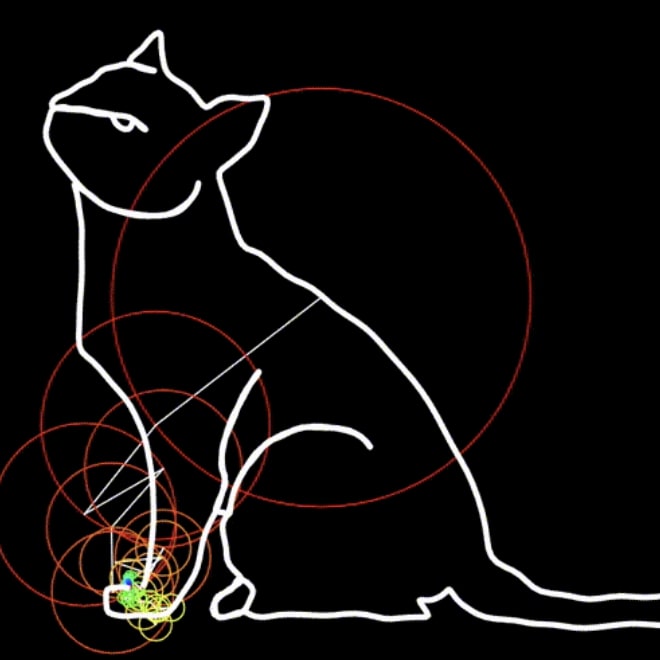
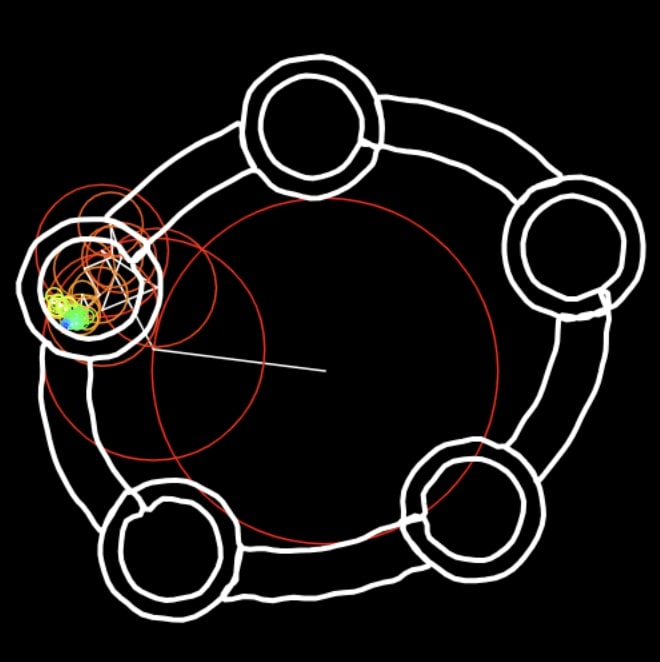
More applets
Here are more fun interactive applets that you can play with. Just click on the image to open the live demo! Enjoy! 😃
Further reading
- Brigham, E. O. (1988). The fast Fourier transform and its applications. Prentice-Hall, Inc. USA.
- Cooley, J. W. and Tukey, J. W. (1965). An algorithm for the machine calculation of complex fourierseries. Mathematics of Computation, 19:297-301.
- Ginnobili, S. and Carman, C. C. (2008). Deferentes, epiciclos y adaptaciones. Associacao de Filosofiae Historia da Ciencia do Cone Sul (AFHIC), 5:399-408.
- Hanson, N. R. (1965). The mathematical power of epicyclical astronomy. Isis, 51:150-158.
- Ponce Campuzano, J. C. (2023). Tracing closed curves with epicycles: A fun application of the Discrete Fourier Transform. North American GeoGebra Journal. Vol 11. No. 1. pp. 1-14.
- Ponce Campuzano, J. C. (2022). Trigonometric intepolation using the Discrete Fourier Transform. North American GeoGebra Journal. Vol. 10. No. 1. pp. 1-13.
- Sundararajan, D. (2018). Fourier Analysis - A Signal Processing Approach. Springer Singapur.
- Stein, E. M. and Shakarchi, R. (2003). Fourier Analysis: An Introduction. Princeton University PressOxford.